Answer: -4.4 m/s
Step-by-step explanation:
This problem can be solved by the Conservation of Momentum principle, which establishes that the initial momentum
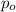 must be equal to the final momentum
must be equal to the final momentum
 :
:
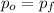 (1)
(1)
Where:
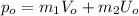 (2)
(2)
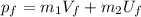 (3)
(3)
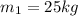 is the mass of the child
is the mass of the child
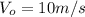 is the initial velocity of the child
is the initial velocity of the child
 is the mass of the adult
is the mass of the adult
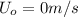 is the initial velocity of the adult (it is sitting still)
is the initial velocity of the adult (it is sitting still)
 is the final velocity of the child
is the final velocity of the child
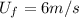 is the final velocity of the adult
is the final velocity of the adult
Substituting (2) and (3) in (1):
 (4)
(4)
Isolating
 :
:
 (5)
(5)
 (6)
(6)
Finally:
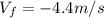 This means the velocity of the child is in the opposite direction
This means the velocity of the child is in the opposite direction