Answer:
The velocity of wind is 34.88 miles per hour
Explanation:
Given as :
The velocity of plane = 190 miles per hour
Let The velocity of wind = w miles per hour
The distance cover by plane = 500 miles
The time taken to cover 500 miles with the wind = t hours
The time taken to cover 500 miles against the wind = ( 1 + t ) hours
Now , Speed =
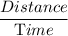
Now, With the wind
190 + w =
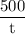
or, t =
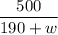
And Against the wind
190 - w =
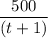
Solving the equation
I.e ( 190 - w ) ( t + 1 ) = 500
or, ( 190 - w ) (
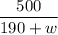 + 1 ) = 500
+ 1 ) = 500
Or, ( 190 - w ) [ 500 + ( 190 + w ) ] = 500 ( 190 + w )
Or, 500 × 190 + 190 × ( 190 + w ) - 500 w - w × ( 190 + w ) = 500 × 190 + 500 w
or, 190 × ( 190 + w ) - 500 w - w × 190 - w² = 500 w
or, 190² + 190 w - 500 w - 190 w - w² = 500 w
or, - w² - 1000 w + 190² = 0
Or , w² + 1000 w - 36100 = 0
Solving this quadratic equation
w =
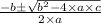
Or, w =
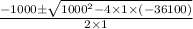
Or, w =
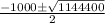
∴ w =
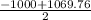 ,
,
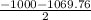
or, w = 34.88 mph , - 1034.88 mph
So, The wind velocity = w = 34.88 mph
Hence The velocity of wind is 34.88 miles per hour Answer