Answer:
The value of given trigonometrical expression is cos²x + sin²x = 1
Explanation:
Given trigonometrical expression as :
(
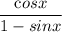 ) - sec x = tan x
) - sec x = tan x
Or, (
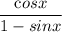 ) = tan x + sec x
) = tan x + sec x
or, (
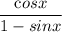 ) = (
) = (
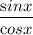 ) + (
) + (
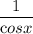 )
)
or, (
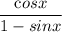 ) = (
) = (
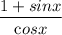 )
)
Now, cross multiplying both side
I.e (cos x) × (cos x) = ( 1 - sin x ) × ( 1 + sin x )
or, cos²x = 1 - sin² x
or, cos²x + sin²x = 1
So, Value of expression is cos²x + sin²x = 1
Hence The value of given trigonometrical expression is cos²x + sin²x = 1 answer