Answer:
a) 9.6 m/s
b) 11.7 m/s
c) 12 m/s
Step-by-step explanation:
This problem can be solved by the Conservation of Momentum principle, which establishes that the initial momentum
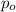 must be equal to the final momentum
must be equal to the final momentum
 :
:
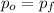 (1)
(1)
Where:
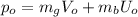 (2)
(2)
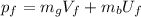 (3)
(3)
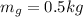 is the mass of green ball
is the mass of green ball
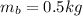 is the mass of the blue ball
is the mass of the blue ball
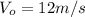 is the initial velocity of the green ball
is the initial velocity of the green ball
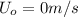 is the initial velocity of the blue ball
is the initial velocity of the blue ball
 is the final velocity of the green ball
is the final velocity of the green ball
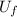 is the final velocity of the blue ball
is the final velocity of the blue ball
Substituting (2) and (3) in (1):
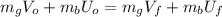 (4)
(4)
Isolating
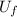 :
:
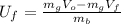 (5)
(5)
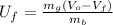 (6) This is the equation we will use for the next cases
(6) This is the equation we will use for the next cases
Knowing this, let's begin with the answers:
a) In this case
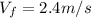 and we have to find
and we have to find
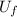
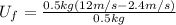 (7)
(7)
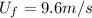 (8)
(8)
b) In this case
 and we have to find
and we have to find
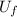
 (9)
(9)
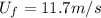 (10)
(10)
c) In this case
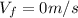 and we have to find
and we have to find
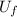
 (11)
(11)
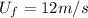 (12)
(12)