Answer:
The Time in which sum of money double itself is 14 years .
Explanation:
Given as :
The principal money = P
The rate of interest = R = 5 % payable half yearly
The Amount = Double of principal
Let The time in which sum become double = t years
I.e A = 2 P
From Compounded method
Amount = principal ×
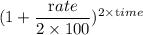
or, 2 P = P ×
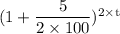
Or, 2 =

Or, Taking log with base 10 both side
So,
 2 =
2 =


or, 0.3010 = 2 t ×
 1.025
1.025
Or, 0.3010 = 2 t × 0.010723
Or, 0.3010 = 0.021446 t
∴ t =
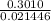
I.e t = 14.03 years ≈ 14 years
So, The time period = T = 14 years
Hence The Time in which sum of money double itself is 14 years . Answer