Question

Determine the total revenue earned by selling x calculator if the price per calculator is given by the demand function p = 150 - 0.4x. How many calculators must be sold to maximize the total revenue?

Answer 1

The revenue is maximum around 187.5 that means we can sell 187 or 188 calculators to get the maximum revenue.

Explanation:

Let the total number of calculators sold = x

The price per demand of calculator , p =150 - 0.4x

Total revenue =
`number of calculators sold * price of each`

=
`x * (150 - 0.4x)`

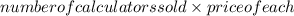
To maximize revenue, derivative of total revenue must be zero.

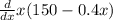`(d)/(dx) x(150 - 0.4x)` = 0

150 - 0.4x - 0.4x = 0

150 - 0.8x = 0

0.8x = 150

x = 187.5

So the revenue is maximum around 187.5 that means we can sell 187 or 188 calculators to get the maximum revenue.

Maximum revenue =
`188 * (150 - 0.4 * 188)`

=14,062.4