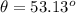Question

a projectile is fired in such away that its horizontal range is equal to three times its naximum height.what is the angle of projection?​

Answer 1

`\theta=53.13^o`

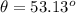
Step-by-step explanation:

2-D Projectile Motion

In 2-D motion, there are two separate components of the acceleration, velocity and displacement. The horizontal component has zero acceleration, while the acceleration in the vertical direction is always the acceleration due to gravity. The basic formulas for this type of movement are

`V_x=V_(ox)=V_ocos\theta`

`V_y=V_(oy)-gt=V_osin\theta-gt`

`x=V_(ox)t`

`\displaystyle y=y_o+V_(oy)t-(gt^2)/(2)`

`\displaystyle x_(max)=(2V_(ox)V_(oy))/(g)`

`\displaystyle y_(max)=(V_(oy)^2)/(2g)`

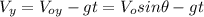
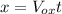
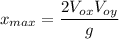
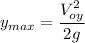
The projectile is fired in such a way that its horizontal range is equal to three times its maximum height. We need to find the angle \theta at which the object should be launched. The range is the maximum horizontal distance reached by the projectile, so we establish the base condition:

`x_(max)=3y_(max)`

`\displaystyle (2V_(ox)V_(oy))/(g)=3(V_(oy)^2)/(2g)`

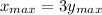
Using the formulas for
`V_(ox), V_(oy):`

`\displaystyle (2V_(o)cos\theta V_(o)sin\theta)/(g)=3(V_(o)^2sin^2\theta)/(2g)`

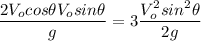
Simplifying

`4cos\theta sin\theta=3sin^2\theta`

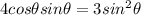
Dividing by
`sin\theta`

`4cos\theta=3sin\theta`

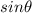
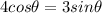
Rearranging

`tan\theta=(4)/(3)`

`\theta=arctan(4)/(3)`

`\theta=53.13^o`