Question

A motorboat can maintain a constant speed of 25 miles per hour relative to the water. The boat makes a trip upstream to a certain point in 48 minutes; the return trip takes 27 minutes. What is the speed of the current?

Answer 1

The speed of the current is 7 miles per hour .

Explanation:

Given as :

The speed of motorboat = x = 25 miles per hour

The Time taken to make upstream trip = 48 minute =
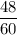`(\textrm 48)/(\textrm 60 )` = 0.8 hour

And The time taken to make downstream trip = 27 minutes =
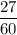`(\textrm 27)/(\textrm 60 )` = 0.45 hour

Let The speed of the current = y miles per hour

Let The total distance cover = D miles

Now, Speed =
`(\textrm Distance)/(\textrm Time)`

So , For upstream trip

x - y =
`(\textrm D)/(\textrm 48 min)`

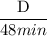
Or, D =
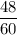`(\textrm 48)/(\textrm 60 )` × ( x - y ) ........1

And , For downstream trip

x + y =
`(\textrm D)/(\textrm 27 min)`

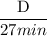
Or, D =
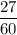`(\textrm 27)/(\textrm 60 )` × ( x + y ) .......2

Now, equating the eq 1 and 2

I.e 0.8 × ( x - y ) = 0.45 × ( x + y )

Or, 0.8 x - 0.8 y = 0.45 x + 0.45 y

Or, 0.8 x - 0.45 x = 0.8 y + 0.45 y

or, 0.35 x = 1.25 y

Now since x = 25 miles per hour

So, 0.35 × 25 = 1.25 y

or, y =
`(0.35* 25)/(1.25)`

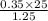
∴ y = 7

So, The speed of current = 7 miles per hour

Hence The speed of the current is 7 miles per hour . Answer