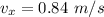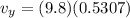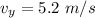Answer:
a. 0.5307 sec
b. 0.4458 m
c. =
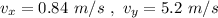
Step-by-step explanation:
Horizontal Motion
It describes the dynamics of an object thrown horizontally in free air. The initial horizontal velocity is maintained all the time since no horizontal forces are acting. The initial vertical velocity is zero at launch time, but it grows downwards powered by the acceleration of gravity.
The object hits the ground at a distance x from the point of launching, after having traveled a vertical distance
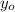 , taking a time t to complete the travel. The formulas who relate the different magnitudes are
, taking a time t to complete the travel. The formulas who relate the different magnitudes are
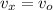
The horizontal velocity
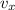 is the same regardless of the elapsed time
is the same regardless of the elapsed time
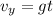
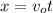
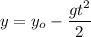
The plate of apple pie left the counter at a speed
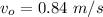
The counter is
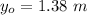 high.
high.
a.
Knowing that
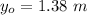
We use this formula to compute t
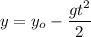
At the moment when the plate hits the floor y=0
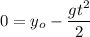
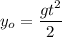
Solving for t
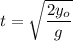
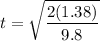
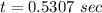
b.
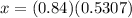
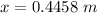
c.