Question

Arnold buys 3 3/5

pounds of green grapes for $1.85 per pound. He buys 3 3/5
pounds of red grapes for $2.30 per pound. Which expression can be used to determine the total cost, in dollars, of the grapes Arnold buys?

Answer 1

The expression can be used to determine the total cost, in dollars, of the grapes Arnold buys is given as:

Total cost = cost of green grapes bought + cost of red grapes bought

The total cost in dollars is $ 14.94

Solution:

Given that Arnold buys
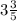`3 (3)/(5)` pounds of green grapes for $1.85 per pound.

Also given that He buys
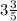`3(3)/(5)` pounds of red grapes for $2.30 per pound.

To find: total cost in dollars of the grapes Arnold buys

Cost of green grapes bought:

Arnold buys
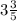`3 (3)/(5)` pounds of green grapes for $1.85 per pound.

Cost per pound = $ 1.85

So cost of
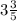`3 (3)/(5)` pounds of green grapes for $1.85 per pound is given as:

`\rightarrow 3 (3)/(5) * 1.85\\\\\rightarrow (18)/(5) * 1.85\\\\\rightarrow 3.6 * 1.85 = 6.66`

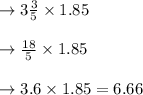
Thus total cost for buying green grapes = $ 6.66

Cost of red grapes bought:

Arnold buys
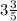`3(3)/(5)` pounds of red grapes for $2.30 per pound.

Cost per pound = $ 2.30

So cost of
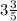`3(3)/(5)` pounds of red grapes for $2.30 per pound is given as:

`\rightarrow 3(3)/(5) * 2.30\\\\\rightarrow (18)/(5) * 2.30\\\\\rightarrow 3.6 * 2.30 = 8.28`

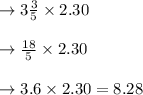
Thus total cost for buying red grapes = $ 8.28

The expression can be used to determine the total cost, in dollars, of the grapes Arnold buys is given as:

Total cost = cost of green grapes bought + cost of red grapes bought

Total cost = $ 6.66 + $ 8.28 = $ 14.94

Thus total cost in dollars is $ 14.94