The co-ordinates of point R is (6 , 2)
Solution:
Given that M(7, 3) is the midpoint of RS
Also co-ordinates of point S is (8, 4)
To find: co-ordinates of point R
The midpoint of two points
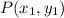 and
and
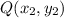 is given as:
is given as:
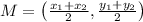
Here midpoint M = (7, 3) and point S
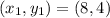
Point R =
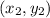
Substituting the values in formula we get,
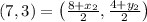
Comparing both the sides we get,
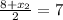 and
and
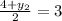
On solving,
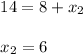
Also,
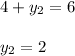
Thus the co-ordinates of point R is (6 , 2)