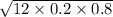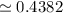Question

-----

r
yuunICUTO!
Question 2: A federal report finds that a lie detector test given to truthful persons
have a probability of 0.2 of suggesting that the person is deceptive. A company
asks 12 job applicants to take a lie detect test. Suppose that all 12 applicants
answer truthfully.
. What is the probability that exactly one is being deceptive?
. What is the probability that at most one is being deceptive?
• What is the mean and standard deviation of this distribution?
I need help with the last two questions.
What is the probability that at most one is being deceptive?
What is the mean and standard deviation of this distribution?

Answer 1

P(Exactly 1 is being deceptive) is
`\simeq` 0.2062 .

P(At most 1 is being deceptive) is
`\simeq 0.2749`

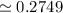
Mean of the distribution is, 2.4 and standard deviation of the distribution is,

`\simeq 0.4382`

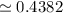
Explanation:

Let, the no. of truthful persons suggested as deceptive by the lie-detector test be denoted by the random variable X. Then, according to the question, in this case,

X
`\sim` Binomial (12, 0.2)

So, here,

1. No. of trials = 12 = n (say)

2. Probability of success = 0.2 = p (say)

3. Probability of failure = (1 - 0.2) = 0.8 = q (say)

So,

P(Exactly 1 is being deceptive)

= P(X = 1)

=
`^(12)C_(1) * (0.2)^(1) * (0.8)^(11)`

`\simeq` 0.2062 ---------------(1)

P(At most 1 is being deceptive)

= P(X = 0) + P(X = 1)

=
`\sum_(x = 0)^(1)(^(12)C_(x)* (0.2)^(x) * (0.8)^((12 - x))`

`\simeq ^(12)C_(0) * (0.2)^(0) * (0.8)^(12) + 0.2062`

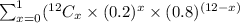
[From (1) putting the value of P(X = 1)]

`\simeq (0.0687 + 0.2062)`

= 0.2749

Mean of the distribution =
`n * p`

=
`12 * 0.2`

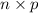
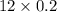
= 2.4

Standard deviation of the distribution,

=
`\sqrt {n * \p * q}`

=
`\sqrt {12 * 0.2 * 0.8}`

`\simeq 0.4382`