Question

Assume you drop a rock from a cliff which is 5000 feet above the ground. The distance in feet, y, of the rock below the cliff at the time t seconds after it was dropped is given by the equation

Y=-1/2gt^2

Answer 1

Explanation:

Given that height of cliff H = 5000 ft

You drop rock from cliff and the distance of rock below the cliff at time,t is given by:

`y= -(1)/(2) gt^(2)`

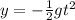
Q1. How far below the cliff is the rock 7 seconds after it dropped ?

Ans. Here, t=7 seconds

By using formula provide, g=32.18 ft{tex]
`s^(-2)`

y=- \frac{1}{2} × 32.17 × (7)^{2}[/tex] = 788.165 ‬ft

Note: Negative sign shows the direction and 240.345 is magnitude

Therefore, Rock is 788.165‬ ft from Cliff

Q2. How far is the rock from the bottom 7 seconds after it dropped ?

By using formula provide,

Ans. After 7 seconds, Rock is 788.165‬ ft from Cliff

Therefore, Rock is 5000-788.165‬ = 4,211.835 ft from bottom

Q3. When will rock hit the bottom?

Ans. Height of cliff H= 5000 ft

Using formula provided, g=32.18 ft
`s^(-2)`

`y = -(1)/(2) gt^(2)`

`-5000 = - (1)/(2) 32.18 × t^(2)`

`t^(2) = (5000×2)/(32.18)`

`t^(2) = 311.13876`

`t = 17.6s`

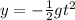
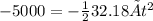
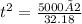
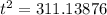
Q4. The Velocity of the rock at impact?

Ans. Velocity is given as V= g×t

By using formula, We get

V= 32.14 × Total time to reach ground

V= 32.14 × 17.6 = 565.66 ft/s