Question

Find the zeros for the polynomial f(x)=-2(x-1)(x+2)2(x+5)3 and give the multiplicity of each zero​

Answer 1

The zeros are: -5, -2 and 1.

Multiplicity of the zero -5 is three

Multiplicity of the zero -2 is two.

Multiplicity of the zero 1 is one.

Explanation:

The zeros of a polynomial,
`f(x)`, are those values of 'x' for which
`f(x)=0`

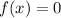
Given:

The polynomial is given as:

`f(x)=-2(x-1)(x+2)^2(x+5)^3`

In order to find its zeros, we need to equate its factors to 0 and determine the values of 'x' for which the function becomes 0.

The factors of the polynomial are
`(x-1),(x+2)^2,(x+5)^3`

So, equating each of them to 0, we get:

`(x+5)^3=0\\(x+5)(x+5)(x+5)=0\\x=-5,-5,-5\\\\(x+2)^2=0\\(x+2)(x+2)=0\\x=-2,-2\\\\(x-1)=0\\x=1`

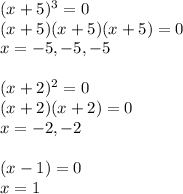
Therefore, the zeros of the polynomial are -5, -2 and 1 with -5 repeated 3 times, -2 repeated 2 times and 1 occurring only once.

So, multiplicity of -5 is 3, multiplicity of -2 is 2 and multiplicity of 1 is 1.