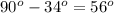Answer:
Option(B) 56. east of north
Step-by-step explanation:
2D Motion
If objects are moving in an XY plane subject to net force (F), acceleration (a), velocity (v) and displacement (r) in both axes, we must consider all those magnitudes as vectors because they have components in x and y.
If
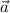 is the acceleration vector, then
is the acceleration vector, then
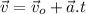
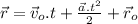
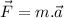
Assuming the positive direction to the right and upwards, we are given the following data
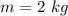
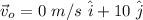
The x-component of the velocity is zero because it due north.
The force is applied eastward;
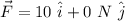
t=3 sec
From the formula
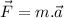
we can solve for
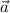
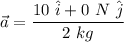
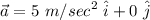
We can now compute the velocity at t=3 sec
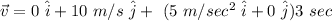
Adding and simplifying
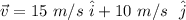
The direction is given by the angle computed as
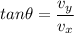
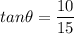
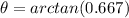
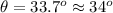
This angle is north of east, the required angle is