Question

In 2018, the population will grow over 700,000.The population of a city in 2010 was 450,000 and was growing at a rate of 5% per year. In what year will the population be over 700,000? Show all work.

Answer 1

The year is 2020.

Explanation:

Let the number of years passed since 2010 to reach population more than 7000000 be 'x'.

Given:

Initial population is,
`P_0=450,000`

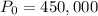
Growth rate is,
`r=5\%=0.05`

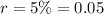
Final population is,
`P=700,000`

A population growth is an exponential growth and is modeled by the following function:

`P=P_0(1+r)^x`

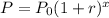
Taking log on both sides, we get:

`\log(P)=\log(P_0(1+r)^x)\\\log P=\log P_0+x\log (1+r)\\x\log (1+r)=\log P-\log P_0\\x\log(1+r)=\log((P)/(P_0))\\x=(\log((P)/(P_0)))/(\log(1+r))`

Plug in all the given values and solve for 'x'.

`x=(\log((700,000)/(450,000)))/(\log(1+0.05))\\x=(0.192)/(0.021)=9.13\approx 10`

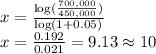
So, for
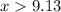`x > 9.13`, the population is over 700,000. Therefore, from the tenth year after 2010, the population will be over 700,000.

Therefore, the tenth year after 2010 is 2020.