Answer :
The value of q for, the given quadratic equation is 40
Step-by-step explanation :
Given quadratic equation as :
x² - 14 x + q = 0
And , Difference between the roots of equation is 6
Let A , B be the roots of the equation
So, A - B = 6
The roots of the quadratic equation ax² + bx + c = 0 as can be find as :
x =
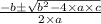
x =
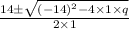
or, x =
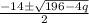
Or, x =
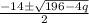
So , The roots are
A =

And B =

∵ The difference between the roots is 6
So, A - B = 6
Or, (
 ) - (
) - (
 ) = 6
) = 6
Or, ( - 7 + 7 ) + 2 (
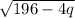 = 6
= 6
Or, 0 + 2 (
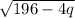 = 6
= 6
∴ 196 - 4 q = 36
or, 4 q = 196 - 36
or 4 q = 160
∴ q =
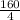
I.e q = 40
S0, The value of q = 40
Hence The value of q for, the given quadratic equation is 40 . Answer