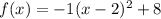Question

Write the quadratic function in standard form.
f(x) = -x2 + 2x + 4
f(x) =

Answer 1

`f(x)=-1(x-2)^2+8`

Explanation:

Given:

The quadratic function is given as:

`f(x)=-x^2+2x+4`

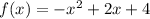
The standard form of a quadratic function is given as:

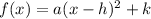`f(x)=a(x-h)^2+k`, where, 'a', 'h' and 'k' are real numbers.

Now, in order to convert the given function to standard form, we use completing by square method.

`-x^2+2x=-(x^2-2x)=-[(x-2)^2-2^2]=-[(x-2)^2-4]=-(x-2)^2+4`

Now,
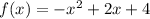`f(x)=-x^2+2x+4` can be rewritten as:

`f(x)=-(x-2)^2+4+4\\f(x)=-1(x-2)^2+8`

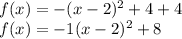
Therefore, the standard form of the function is:

`f(x)=-1(x-2)^2+8`