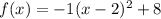Answer:
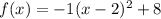
Explanation:
Given:
The quadratic function is given as:
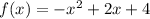
The standard form of a quadratic function is given as:
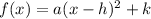 , where, 'a', 'h' and 'k' are real numbers.
, where, 'a', 'h' and 'k' are real numbers.
Now, in order to convert the given function to standard form, we use completing by square method.
![-x^2+2x=-(x^2-2x)=-[(x-2)^2-2^2]=-[(x-2)^2-4]=-(x-2)^2+4](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mdv6rr5emj4i0hmcb4ltei7fpcy3keft71.png)
Now,
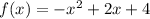 can be rewritten as:
can be rewritten as:
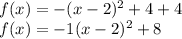
Therefore, the standard form of the function is: