Question

Quadratic function whose zeros are 8 and 3?

Answer 1

The required quadratic function is

`\therefore f(x)=x^(2) -11x+24`

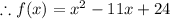
Explanation:

Given:

Let α and β be the zeros of the quadratic function.

∴ α = 8 and

∴ β = 3

To Find :

Quadratic function.

i.e f(x) =?

Solution:

he quadratic function in x when Alpha ( α ) and beta ( β ) are the zeros given by

`f(x) = x^(2) -(\alpha+\beta ) x +\alpha* \beta\\\textrm{Substituting alpha and beta we get}\\= x^(2) -(8+3)x + 8* 3\\\\\therefore f(x)=x^(2) -11x+24`

`\therefore f(x)=x^(2) -11x+24`

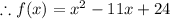
Which is the required quadratic function