Question

A boats sail is a right triangle . The length of one side of the sail is 7 feet more than the other side . The hypotenuse is 13 feet . Find the lengths of the two side of the sails

Answer 1

The lengths of the two side of the sails are 5 feet and 12 feet

Solution:

A boats sail is a right triangle

The diagram is attached below

ABC represents the right angled triangle

AC represents hypotenuse

AC = 13 feet

AB and BC are the other two legs of right angled triangle

Let BC = "a"

So by given length of one side of the sail is 7 feet more than the other side

So AB = a + 7

To find: lengths of the two side of the sails

We have to find length of AB and BC

By pythagoras theorem,

The square of the length of the hypotenuse of a right triangle equals the sum of the squares of the lengths of the other two sides.

So above definition we can say,

`AC^2 = BC^2 + AB^2`

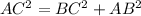
Substituting the above values of AB = a + 7 and BC = "a" and AC = 13

`13^2 = a^2 + (a + 7)^2\\\\169 = a^2 + a^2 + 14a + 49\\\\169 = 2a^2 + 14a + 49\\\\2a^2 + 14a - 120 = 0`

Dividing each term by 2

`a^2 + 7a - 60 = 0`

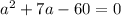
Using factoring method to solve this quadratic equation,

"7a" can be written as 12a - 5a

`a^2 + 12a - 5a - 60 = 0`

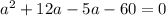
Taking "a" as common from first two terms and -5 as common term from next two terms

a(a + 12) -5(a + 12) = 0

Taking (a + 12) as common term,

(a + 12)(a - 5) = 0

Equating each term to zero,

a + 12 = 0 or a - 5 = 0

a = -12 or a = 5

Since length cannot be negative, so ignore a = -12

Thus length of BC = "a" = 5

And length of AB = a + 7 = 5 + 7 = 12

Thus the lengths of the two side of the sails are 5 feet and 12 feet