Question

Passing through(-1,8) and parallel to the line whose equation is 8x-9y-2=0

Answer 1

y = 8/9x + 80/9

Explanation:

We are given;

• Equation of a line as 8x -9y -2 = 0
• Coordinates (-1,8)

We are required to determine the equation of a line parallel to the given line and passing through a point (-1,8)

Step 1: Determine the Gradient of the given line

• When an equation is written in the form y = mx + c, m is the gradient.
• Therefore; we could write the equation 8x -9y -2 = 0 in the form of y= mx + c

9y = 8x -2

y = 8/9x - 2/9

Therefore, the slope, m = 8/9

Step 2: Determine the equation of the line

• We need to know that parallel lines have the same gradient
• Therefore, the slope of the line in question is 8/9
• It passes through a point (-1, 8)

We can therefore, determine the equation;

Taking another point, (x,y)

`(y-8)/(x+1) = (8)/(9)`

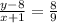
9(y-8) = 8(x+1)

9y - 72 = 8x + 8

9y = 8x + 8 +72

9y = 8x + 80

y = 8/9x + 80/9

Therefore, the equation of the line is y = 8/9x + 80/9