Answers:
a) -2.54 m/s
b) -2351.25 J
Step-by-step explanation:
This problem can be solved by the Conservation of Momentum principle, which establishes that the initial momentum
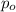 must be equal to the final momentum
must be equal to the final momentum
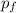 :
:
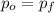 (1)
(1)
Where:
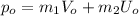 (2)
(2)
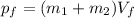 (3)
(3)
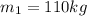 is the mass of the first football player
is the mass of the first football player
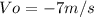 is the velocity of the first football player (to the south)
is the velocity of the first football player (to the south)
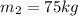 is the mass of the second football player
is the mass of the second football player
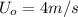 is the velocity of the second football player (to the north)
is the velocity of the second football player (to the north)
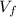 is the final velocity of both football players
is the final velocity of both football players
With this in mind, let's begin with the answers:
a) Velocity of the players just after the tackle
Substituting (2) and (3) in (1):
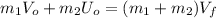 (4)
(4)
Isolating
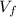 :
:
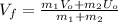 (5)
(5)
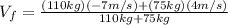 (6)
(6)
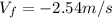 (7) The negative sign indicates the direction of the final velocity, to the south
(7) The negative sign indicates the direction of the final velocity, to the south
b) Decrease in kinetic energy of the 110kg player
The change in Kinetic energy
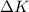 is defined as:
is defined as:
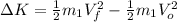 (8)
(8)
Simplifying:
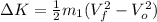 (9)
(9)
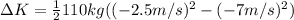 (10)
(10)
Finally:
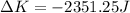 (10) Where the minus sign indicates the player's kinetic energy has decreased due to the perfectly inelastic collision
(10) Where the minus sign indicates the player's kinetic energy has decreased due to the perfectly inelastic collision