Answer:
The possible values of n for n ≤ +4 = (-∞,+4]
The possible values of n for n ≤ -4 = (-∞,-4]
Explanation:
Here, the given inequality is:
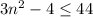
Firstly, let us solve the given inequality for the desirable value of n.
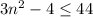
Adding 4 on both sides, we get:


or,
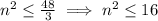
⇒ n ≤ +4 or n ≤ -4
So, the possible values of n for n ≤ +4 = (-∞,+4]
And, the possible values of n for n ≤ -4 = (-∞,-4]
So, we can pick any of the integer values from the both defined sets.