Question

Find the length of the shorter leg of a right triangle with the longer leg is 9 feet more than the shorter leg the hypotenuse is nine feet less than twice the shorter leg

Answer 1

Length of Shorter leg = 27 feet

Length of Longer leg = 36 feet

Length of Hypotenuse = 45 feet

Explanation:

Given:

Let,

Length of Shorter leg = x,

According to the given condition we have

∴ Length of Longer leg = x + 9 feet

∴ Length of Hypotenuse = 2x - 9 feet

To Find:

Length of Shorter leg = ?

Solution:

Now In Right Angle Triangle, By Pythagoras theorem we have

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

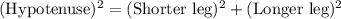
substituting the given values we get

`(2x-9)^(2) = (x)^(2)+(x+9)^(2)\\`

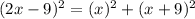
By using Identity (A ± B)² = A² ± 2AB +B² we get

`4x^(2) -36x+81=x^(2) +(x^(2) +18x+81)\\\\4x^(2) -2x^(2) -36x-18x=81-81\\\\2x^(2) -54x=0\\2x(x-27)=0\\2x=0 or x-27=0\\\therefore x\ cannot\ be \ zero\\\therefore x = 27 \feet`

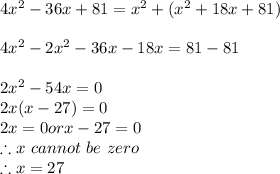
Substituting x=27 we get

∴ Length of Longer leg = x + 9 =27 +9 = 36 feet

∴ Length of Hypotenuse = 2x - 9 = 2×27 -9 = 45 feet