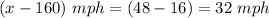Question

A passenger train leaves the station 1 hour after a freight train leaves the same station. The freight train is traveling 16 mph slower than the passenger train. Find the rate of both trains if it takes 2 hours for the passenger train to overtake the freight train.

Answer 1

Rate of the passenger train is
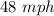`48\ mph` and the rate of the freight train is
`32\ mph`

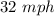
Explanation:

Let the speed of the passenger train be
`x\ mph`

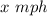
Speed of the freight train be
`(x-16)\ mph`

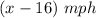
Note:

If the passenger train overtakes the freight train than at the point both have traveled same distance as they are from the same station.

And
`Distance=Speed* time`

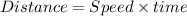
Time taken by the passenger train to reach that point
`=2\ hrs`

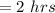
Time taken by freight train,= (time taken by the passenger train + time elapsed)
`=(2+1)=3\ hrs`

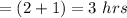
Re-arranging the terms.

Distances are same.

`3(x-16)=2(x)`

`3x-48=2x`

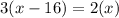
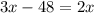
Subtracting
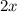`2x` both sides.

`3x-2x=48`

`x=48\ mph`

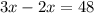
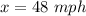
So the rate of the passenger train is
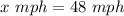`x\ mph=48\ mph` and the rate of the freight train is
`(x-160)\ mph =(48-16)=32\ mph`