Question

Sinxcos y = 1/2(sin(x + y) + cos(x - y)) TRUE OR FALSE

Answer 1

False

sin x cos y
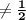`\\eq(\bf 1)/(\bf 2)` (sin (x + y) + cos (x - y))

Explanation:

Given
`\sin x \cos y = 1/2(\sin(x + y) + \cos(x - y))\hfill (1)`

To verify that the equality is true or false

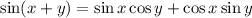`\sin (x+y)=\sin x \cos y+ \cos x \sin y` and

`\cos (x-y)=\cos x \cos y+ \sin x \sin y`

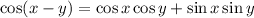
Now adding the above equations we get

`\sin (x+y)+ \cos (x-y)= \sin x \cos y+ \cos x \sin y+ \cos x \cos y+ \sin x \sin y\hfill (2)`

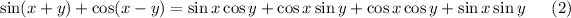
Comparing the equations (1) and (2) we get

`\sin x \cos y \\eq \frac {1}{2} \(sin (x + y) + \cos (x - y))`

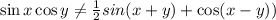
Therefore the given equality is not true (ie, false)