Question

The relationship between altitude and the boiling point of a liquid is linear. At an altitude of 8500 ​ft, the liquid boils at 199.95 degrees F. At an altitude of 4300 ​ft, the liquid boils at 205.41 degrees F. Write an equation giving the boiling point b of the​ liquid, in degrees​ Fahrenheit, in terms of altitude​ a, in feet. What is the boiling point of the liquid at 2600 ​ft?

Write an equation.
(Use integers or decimals for any numbers in the​ expression.)

Answer 1

b = -0.0013a + 211

Explanation:

Since the relationship is linear, we can use a linear equation. The formula in slope-intercept form is
`y = mx + b`.

As the question specifies to use a for altitude and b for boiling point, change the variables equation to
`b = ma + c`

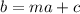
b is the boiling point.

m is the slope.

a is the altitude.

c is the y-intercept.

To find the slope, we can use the equation
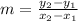`m = (y_(2) - y_(1)  )/(x_(2) - x_(1) )` except x is a and y is b.

The sets of information given are:

8500 ​ft, the liquid boils at 199.95° (This can be info set 1)

4300 ​ft, the liquid boils at 205.41° (This can be info set 2)

Substitute the info sets into the equation. The subscripts mean which info set to get the numbers from.

`m = (b_(2) - b_(1)  )/(a_(2) - a_(1) )`

`m = (205.41 - 199.95 )/(4300 - 8500)`

`m = (5.46 )/(-4200)`

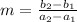
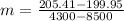
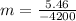
m = -0.0013

Find the y-intercept by substituting m = -0.0013 and a random info set. I will use info set 1. Isolate c, the only variable.

b = ma + c

199.95 = (-0.0013)(8500) + c <= Simplify

199.95 = -11.05 + c

199.95 + 11.05 = -11.05 + 11.05 + c <=add 11.05 on both sides to isolate c

c = 211 <= y-intercept

Put the y-intercept and slope into the equation of a line:

b = ma + c

b = -0.0013a + 211 <= This is the equation for the problem.