Question

Given the following information about glucose levels (in milligrams of glucose per 100 milliliters of blood.) ( from 9.5)

col1 73 61 104 75 85 65 62 98 92 106 ( Non pregnant women)

col2 72 84 90 95 66 70 79 85 (pregnant women)

A. Find the sample standard deviation s of the non pregnant women sample
B. Find the sample standard deviation s of the pregnant women sample.
C. CLAIM: " The variance of the glucose test results for non pregnant women is different to the variance for pregnant women"

NOTATION: sigma squared is the population variance. (choose from 4 options below)

a. sigma squared of non pregnant women is GREATER THAN sigma squared of non pregnant women
b.sigma squared of non pregnant women IS equal to sigma squared of non pregnant women
c. sigma squared of non pregnant women is NOT equal to sigma squared of non pregnant women
d. sigma squared of non pregnant women is LESS THAN sigma squared of non pregnant women

Answer 1

A. 16.385

B. 9.532

C. (16.358)^2 is different from (9.532)^2

a. sigma squared of non pregnant women is GREATER THAN sigma squared of pregnant women

Explanation:

A and B. Standard Deviation 's' of both columns:

The formula for the standard deviation is:

s = √(∑(x - μ)²/(n))

where,

∑ = is the sum function

x = a number from the set

μ = mean of the set

n = is the amount of the numbers in the set.

the column of non-pregnant women is

[73, 61, 104, 75, 85, 65, 62, 98, 92, 106]

• first find the mean of this set:

mean = μ = (sum of all the numbers)/(amount of numbers)

μ = [73 + 61 + 104 +75 + 85 + 65 + 62 + 98 + 92 + 106]/(10)

μ = 821/10

μ = 82.1

similarly, for pregnant women the mean is

μ = 80.125

• now, to find the standard deviation 's', first we need to find the variance 's²'. So, what you have to do is subtract each value in the column with the mean 'μ' and square the result.

for non-pregnant you will get:

[ 82.81, 445.21, 479.61, 50.41, 8.41, 292.41, 404.01, 252.81, 98.01, 571.21]

for pregnant you will get:

[ 66.015, 15.015, 97.515, 221.265, 199.51, 102.515, 1.265, 23.76]

• finally just sum all the numbers of a column and divide with the amount of numbers in that column (remember that col1 has 10 numbers and col2 has 8 numbers). And you will get your variance for both pregnant and non-pregnant women:

for non-pregnant = 2684.89/10

non-pregnant = 268.4 (this is the variance and it is denoted by s²)

for standard deviation 's', just take the square root of the variance

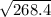`√(268.4)` = 16.385.

similarly standard deviation of pregnant women can be found to be:

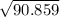`√(90.859)` = 9.532.

A. non-pregnant 'S' = 16.385

B. pregnant 'S' = 9.532

C. CLAIM:

you only have to show whether the variance of the above two columns are different or not.

And YES, the variances of the two column are indeed different, hence you make the CLAIM as written in question(C)

Multiple Choice:

here you need to show how different are the two values:

recall the variances:

Column1 = 268.4 (non-pregnant)

Column2 = 9.532 (pregnant)

now you know that the variance of non-pregnant is GREATER THAN the variance of pregnant