Question

. Wilson Publishing Company produces books for the retail market. Demand for a current book is expected to occur at a constant annual rate of 7200 copies. The cost of one copy of the book is $14.50. The holding cost is based on an 18% annual rate, and production setup costs are $150 per setup. The equipment on which the book is produced has an annual production volume of 25,000 copies. Wilson has 250 working days per year, and the lead time for a production run is 15 days. Use the production lot size model to compute the following values:

a. Minimum cost production lot size
b. Number of production runs per year
c. Cycle time
d. Length of a production run
e. Maximum inventory
f. Total annual cost
g. Reorder point

Answer 1

(a) 1,078.12 copies

(b) 6.68 runs per year

(c) 37.43 days

(d) 10.78 days

(e) 767.62 copies

(f) $2,003.48

(g) 432 copies

Given Data:

Annual demand (D) = 7200 copies

Cost of the book (C) = $14.50

Holding cost (H) = 18% of cost of book = ($14.50)*18% = $2.61

Setup costs (S) = $150

Annual production volume (P) = 25,000 copies

Number of working days (n) = 250

Lead time (L) = 15 days

Calculations:

(a) Minimum cost production lot size (Q):

`Q=\sqrt{(2*D*S)/(H*(1-(D)/(P)) ) } \\\\Q=\sqrt{(2*(7200)*(150))/((2.61)*(1-(7200)/(25000)) ) }\\\\`)

Q = 1,078.12 copies

(b) Number of production runs (PR):

`PR = (D)/(Q)\\\\PR = (7200)/(1078.12)\\\\`

PR = 6.68 runs annually

(c) Cycle time (
`T_c`):

`T_c = n*((Q)/(D))\\\\T_c = 250*((1078.12)/(7200))\\\\`

`T_c` = 37.43 days

(d) Length of a production run (PRL):

`PRL=n*((Q)/(P))\\\\PRL=250*((1078.12)/(25000))\\\\`

PRL = 10.78 days

(e) Maximum inventory (
`I_(max)`):

`I_(max) = (1-(D)/(P))*Q\\\\I_(max) = (1-(7200)/(25000))*1078.12`

`I_(max)` = 767.62 copies

(f) Total annual cost (TAC):

TAC = Annual holding cost + Annual setup cost -------------------- (1)

where,

Annual holding cost =
`((1)/(2))*I_(max)*H\\\\`

Annual holding cost =
`((1)/(2))*767.62*2.61\\\\`

Annual holding cost = $1001.74

and,

Annual setup cost =
`((D)/(Q))*S\\\\`

Annual setup cost =
`((7200)/(1078.12))*150\\\\`

Annual setup cost = $1,001.74

Equation (1) will become,

TAC = $1,001.74 + $1,001.74

TAC = $2,003.48

(g) Reorder point (R):

`R = ((D)/(n))*L\\\\R = ((7200)/(250))*15\\\\`

R = 432 copies

Answer 2

(a) 1,078.12 copies

(b) 6.68 runs per year

(c) 37.43 days

(d) 10.78 days

(e) 767.62 copies

(f) $2,003.48

(g) 432 copies

Step-by-step explanation:

Given that,

Annual demand (D) = 7200 copies

Cost of the book (C) = $14.50

Holding cost (H) = 18% of cost of book = 18% of $14.50

= $2.61

Setup costs (S) = $150

Annual production volume = 25,000 copies

Number of working days = 250

Lead time (L) = 15 days

Daily demand (d) = Annual demand ÷ Number of working days

= 7200 ÷ 250

= 28.8 copies

Daily production (p) = Annual production ÷ Number of working days

= 25000 ÷ 250

= 100 copies

(a) Minimum cost production lot size (Q):

`Q=\sqrt{(2* D* S)/(H* (1-(d)/(p)))}`

`Q=\sqrt{(2* 7,200* 150)/(2.61* (1-(28.8)/(100)))}`

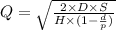
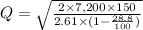
Q = 1,078.12 copies

(b) Number of production runs:

= Annual demand (D) ÷ Production quantity (Q)

= 7,200 ÷ 1,078.12

= 6.68 runs per year

(c) Cycle time:

= Production quantity (Q) ÷ Daily demand (d)

= 1,078.12 ÷ 28.8

= 37.43 days

(d) Length of a production run:

= Production quantity (Q) ÷ Daily production (p)

= 1,078.12 ÷ 100

= 10.78 days

(e) Maximum inventory (Imax):

= Q × (1 - d÷p)

= 1,078.12 × (1 - 28.8 ÷ 100)

= 767.62 copies

(f) Total annual cost:

= Annual holding cost + Annual setup cost

= [(Q ÷ 2) × H × (1 - d÷ p)] + [(D ÷ Q) × S]

= [(1,078.12 ÷ 2) × $2.61 × (1 - 28.8 ÷ 100)] + [(7,200 ÷ 1,078.12) × $150]

= $1,001.74 + $1,001.74

= $2,003.48

(g) Reorder point:

= Daily demand × Lead time

= 28.8 × 15

= 432 copies