A torsion pendulum consists of an irregularly-shaped object of mass 29.0 kg suspended vertically by a wire of torson constant 1.14 Nm through its center of mass. If this pendulu…

Question

asked Oct 21, 2020 170k views

1 Answer

Charles Holbrow · Answer 1 · 2020-10-27T00:16:57+0000

Answer:

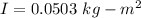
$I=0.0503\ kg-m^2$

Step-by-step explanation:

Given that,

Mass of the object, m = 29 kg

Torsion constant of the wire, K = 1.14 N-m

Number of cycles, n = 98

Time, t = 74 s

To find,

The rotational inertia of the object.

Solution,

Relationship between the moment of inertia, time period and the torsion constant of the spring is given by :

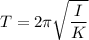
$T=2\pi\sqrt{(I)/(K)}$

Where I is the moment of inertia

K is spring constant

Let T Is the time period of oscillation, such that,

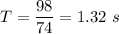
$T=(98)/(74)=1.32\ s$

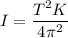
$I=(T^2K)/(4\pi ^2)$

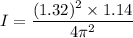
$I=((1.32)^2* 1.14)/(4\pi ^2)$

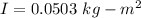
$I=0.0503\ kg-m^2$

So, the rotational inertia of the object is
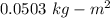$0.0503\ kg-m^2$ .