Question

The rectangle below has an area of x2 + 11x + 28 square meters and a length of 2 + 7 meters.

What expression represents the width of the rectangle?
2 + 7
Width
x2 + 11x + 28

Answer 1

Question:

The rectangle below has an Área of x^2 + 11x + 28 square meters and a length of x+7 meters. What expression represents the width of the rectangle?

Answer:

The expression representing width of rectangle is (x + 4) meters

Solution:

Given that rectangle has an area x^2 + 11x + 28 square meters and a length of x + 7 meters

To find: width of the rectangle

The area of rectangle is given as:

`\text {Area of rectangle }=\text { length } * \text { width }`

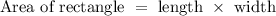
Here area = x^2 + 11x + 28 square meters

length = x + 7 meters

Substituting the values in given formula,

`\begin{array}{l}{\text { width }=(x^(2)+11 x+28)/(x+7)} \\\\ {\text { width }=(x^(2)+4 x+7 x+28)/(x+7)} \\\\ {\text { width }=(x(x+4)+7(x+4))/(x+7)} \\\\ {\text { width }=((x+4)(x+7))/(x+7)}\end{array}`

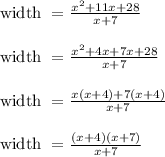
Cancelling (x + 7) on numerator and denominator,

`\text { width }=(x+4)`

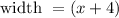
Thus expression representing width of rectangle is (x + 4) meters