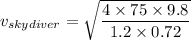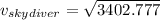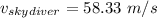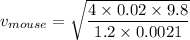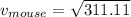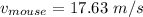Answer
given,
mass of the skydiver = 75 Kg
mass of pet = 20 g
to find the terminal speed of both the sky diver and the mouse
Using terminal speed formula
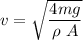
ρ is the density of the air
A is the area of mouse and skydiver
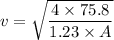
Assuming area of Skydiver = 0.72 m²
and Area of mouse will be equal to = 0.0021 m²
now,