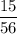Answer: C.
Step-by-step explanation:
Given : Total people = 8
Number of people are to be selected = 3
The number of combinations of r things taken out of n things is given by :-
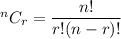
The total number of ways to select 3 people out of 8 is given by :-
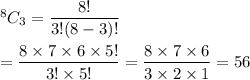
If George is included , then one person is confirmed, so we need to selec only 2 people out of 7.
Also, Nina is not selected , so the total number of people left= 6
The total number of ways to select 2 people out of 6 that will include George but not Nina is given by :-

i.e. No. of favorable outcomes= 15
Now, the probability that 3 people selected will include George but not Nina :-

Hence, the required probability = C.