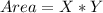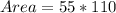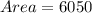Question

A developer wants to enclose a rectangular grassy lot that borders a city street for parking. If the developer has 220 feet of fencing and does not fence the side along the street, what is the largest area that can be enclosed?

a.12100 square feet
B. 6050 square feet
C. None of these.
D. 9075 square feet
E. 3025 square feet

Answer 1

6050 square feet

Explanation:

Based on the diagram attached, the area which the available fencing can enclose will measure X x Y feet. As the total length of fencing available is 220 feet, the fenced perimeter must equal 220 feet

`Y + 2X = 220`

`Y = 220 - 2X`

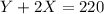
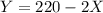
Area of a rectangle is determined by multiplying the length of perpendicular sides:

`Area = X*Y`

`Area = X(220 - 2X)`

`Area = 220X - 2X^(2)`

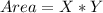
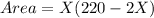
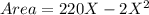
The derivative of an equation determines the slope at any given point of that equation. At the maximum or minimum point of the equation, the slope will be zero. Therefore, differentiating the equation for area and equating it to zero will give the value of X where the area is maximum.

A simple variable can be differentiated using below concept:

`f(a) = a^(b)`

`f'(a) = ba^(b-1)`

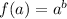
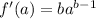
Using the above concepts to differentiate Area and calculate X will give:

`Area = 220X - 2X^(2)`

`Area' = 220 - 4X = 0`

`X = 55`

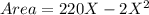
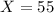
Calculating Y:

`Y = 220 - 2X`

`Y = 220 - 2(55)`

`Y = 110`

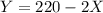
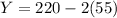
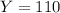
Calculating Area:

`Area = X*Y`

`Area = 55*110`

`Area = 6050\sqfeet`