Question

A 2006 poll asked whether Turkey should be included in the European Union if it met all conditions set by the EU. 51% of respondents from Denmark said "yes". Identify the point estimate and the 95% confidence interval. Then, draw substantive conclusions about the Danish population based on this poll.

Answer 1

Explanation:

Hello!

Your study variable is

X: number of danish that supports the inclusion of Turkey to the EU, of a sample of n people.

This is a discrete variable. It has only two possible outcomes "yes" and "no" and what is of interest is the proportion of danish that voted yes on the poll. (success) The sample size n is fixed since the beginning, the proportion of success is the same from one trial to another and the trials are independent of trial to trial.

The parameter is the population proportion ρ

Its point estimate is the sample proportion ^ρ

If you take the n danish that answered the 2006 poll as the sample, then the sample proportion is ^ρ= 0.51

Applying the Central Limit Theorem you can approximate the sample proportion distribution to normal, and use the Z-statistic to estimate the population proportion with a Confidence Interval.

Z= ^ρ - ρ ≈N(0;1)

√(^ρ(1-^ρ))/n

The formula for the interval:

^ρ ±
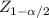`Z_(1-\alpha /2)`*√(^ρ(1-^ρ))/n

Suppose the sample size was n= 500

The Confidence Interval is:

^ρ ±
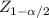`Z_(1-\alpha /2)`*√(^ρ(1-^ρ))/n

`Z_(1-\alpha /2)`=
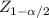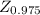`Z_(0.975)` = 1.96

0.51 ± 1.96*√(0.51(1-0.51))/500

[0.4562; 0.5538]

With a Confidence level of 95%, you'd expect that the population proportion of danish that supports Turkey entering the EU is contained by the interval [0.4562; 0.5538].

I hope it helps!