Answer:
1) 80% CI: [3.04; 3.26]gr
d= 0.11
2) n= 28 hummingbirds
Explanation:
Hello!
The study variable of this experiment is:
X: the weight of a hummingbird. (gr)
And it has a normal distribution, symbolically: X~N(μ;σ²)
And (I hope I got it correctly) its population standard deviation is σ= 0.33
There was a sample of n= 15 hummingbirds taken, its sample mean X[bar]= 3.15 gr
1) You need to construct an 80% Confidence Interval for the population mean of the hummingbird's weight.
Since the study variable has a normal distribution, you can use either the standard normal distribution or the Student's t distribution. Both are useful to estimate the population mean. Since the population standard variance is known, the best choice is the Standard normal.
Z= X[bar] - μ ~ N(0;1)
σ/√n
The formula for the interval is:
X[bar] ±
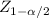 * (σ/√n)
* (σ/√n)
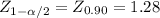
3.15 ± 1.28 * (0.33/√15)
[3.04; 3.26]gr
The margin of error (d) of a confidence interval is hal its amplitude (a)
a= Upper bond - Lower bond
d= (Upper bond - Lower bond)/2
d=
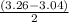 = 0.11
= 0.11
2) You need to calculate a sample size for a 80% Confidence interval for the average weight of the hummingbirds with a margin of error of d= 0.08
As I said before, the margin of error is half the amplitude of the interval, the formula you use to estimate the population mean has the following structure:
"point estamator" ± "margin of error"
Then the margin of error is:
d=
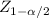 * (σ/√n)
* (σ/√n)
Now what you have to do is rewrite the formula based on the sample size
d=
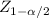 * (σ/√n)
* (σ/√n)
 = σ/√n
= σ/√n
√n *
 = σ
= σ
√n = σ *
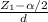
n = (σ *
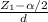 )²
)²
n= (0.33 *
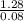 )²
)²
n= 27.8784 ≅ 28 hummingbirds.
I hope it helps!