Question

How many solutions are there to the equation below 6×+30+4×=10(×+3)

Answer 1

Infinite many solutions. Any x-value can satisfy the equation.

Explanation:

Let's work on simplifying the equation a little to investigate which x-values satisfy it. Start by combining like terms on the left side (6x +4x=10x),

then distribute the factor "10" into the binomial (x+10), obtaining 10x +30.

Now we have the same expression on the left and the right of the equal sign:

10x +30=10x+30. We may subtract 30 from both sides, and obtain 10x=10x, and at this point divide by 10 both sides, and we obtain: x=x

The process is shown below.

`6x+30+4x=10(x+3)\\6x+4x+30=10x+30\\10x+30=10x+30\\10x=10x\\x=x`

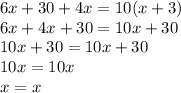
x=x is an equation that is verified by absolutely ANY x value on the number line, and there are infinite x-values in the number line.

Therefore there are infinite many solutions to this equation (any x-value will satisfy it).