Question

A ball is shot from the ground into the air. At a height of 8.8 m, the velocity is observed to be

v = (7.7)i + (5.7)j in meters per second (i horizontal, j upward). To what maximum height will the ball rise?

What will be the total horizontal distance traveled by the ball?
What is the velocity of the ball (magnitude and direction) the instant before it hits the ground? That is what is its i-component?
What is its j-component?

Answer 1

h = 10.4 m

R = 22.48 m

v= 16,2 m/s , α = 61.7°, below the horizontal

v = (7.7)i + (-14.3)j in meters per second (i horizontal, j downward)

Step-by-step explanation:

The ball describes a parabolic path, and the equations of the movement are:

Equation of the uniform rectilinear motion (horizontal ) :

x = vx*t :

Equations of the uniformly accelerated rectilinear motion of upward (vertical ).

y = (v₀y)*t - (1/2)*g*t² Equation (2)

vfy² = v₀y² -2gy Equation (3)

vfy = v₀y -gt Equation (4)

Where:

x: horizontal position in meters (m)

t : time (s)

vx: horizontal velocity in m

y: vertical position in meters (m)

v₀y: initial vertical velocity in m/s

vfy: final vertical velocity in m/s

g: acceleration due to gravity in m/s²

Known data

y= 8.8 m

v = ( (7.7)i + (5.7)j ) m/s : vx= 7.7 m/s , vy= 5.7 m/s

g = 9.8 m/s²

Calculation of the initial vertical velocity ( v₀y)

We apply Equation (3) with the known data

(vfy)² = (v₀y)² -2*g*y

(5.7)² = (v₀y)²- (2)*(9.8)*(8.8)

(5.7)²+ 172.48 = (v₀y)²

`v_(oy) = \sqrt{(5.7)^(2)+ 172.48 }`

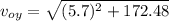
v₀y = 14.3 m/s

Calculation of the maximum height the ball rise (h)

In the maximum height vfy=0

We apply the Equation (3) :

(vfy)² = (v₀y)² -2*g*y

0 = (14.3)² - 2*98*h

h = (14.3)² / 19.6

h = 10.4 m

Calculation of the time it takes for the ball to the maximum height

We apply the Equation (4) :

vfy = v₀y -gt

0 = v₀y -gt

gt = v₀y

t = v₀y/g

t = 14.3/9.8

t= 1.46 s

Flight time = 2t = 2.92 s

Total horizontal distance traveled by the ball (R)

We replace data in the equation (1)

x =vx*t vx= 7.7 m/s , t =2.92 s (Flight time)

R = (7.7)* (2.92) = 22.48 m

Velocity of the ball (magnitude (v) and direction (α)) the instant before it hits the ground

vx = 7.7 m/s

vy = v₀y -gt = 14.3 - 9.8* (2.92) = -14.3 m/s

`v= \sqrt{v_(x)^(2)+v_(y)^(2)  }`

`v= \sqrt{(7.7)^(2)+ (-14.3)^(2)  }`

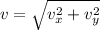
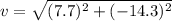
v= 16,2 m/s

`\alpha = tan^(-1) ((v_(y) )/(v_(x) ))`

`\alpha = tan^(-1) ((-14.3 )/(7.7 ))`

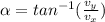
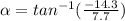
α = -61.7°

α = 61.7°, below the horizontal

i- j components of the v

v = (7.7)i + (-14.3)j in meters per second (i horizontal, j downward)