Question

A researcher used a sample of n = 60 individuals to determine whether there are any preferences among six brands of pizza. Each individual tastes all six brands and selects his/her favorite. If the data are evaluated with a chi-square test for goodness of fit using α = .05, then how large does the chi-square statistic need to be to reject the null hypothesis?

7. A chi-square test for goodness of fit is used to examine the distribution of individuals across four categories, and a chi-square test for independence is used to examine the distribution of individuals in a 2×2 matrix of categories. Which test has the larger value for df?

8. A sample of 100 people is classified by gender (male/female) and by whether or not they are registered voters. The sample consists of 80 females and 20 males, and has a total of 60 registered voters. If these data are used for a chi-square test for independence, what is the total number of females for the expected frequencies?

9. What is stated by the null hypothesis for the chi-square test for independence?

10. A chi-square test for independence is being used to evaluate the relationship between two variables, one of which is classified into 3 categories and the second of which is classified into 4 categories. The chi-square statistic for this test would have df equal to ______.

Answer 1

1) χ² ≥ 11.07

2) Goodness of fit test, df: χ²
`_(3)`

Independence test, df: χ²
`_(1)`

The goodness of fit test has more degrees of freedom than the independence test.

3)
`e_(females.) = 80`

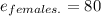
4) H₀:
`P_(ij)= P_(i.) * P_(.j)` ∀ i= 1, 2, ..., r and j= 1, 2, ..., c

5) χ²
`_(6)`

Explanation:

Hello!

1)

The researcher took a sample of n=60 people and made them taste proof samples of six different brands of pizza and choose their favorite brand, their choose was recorded. So the study variable is the following:

X: favorite pizza brand, categorized in brand 1, brand 2, brand 3, brand 4, brand 5 and brand 6.

The Chi-square goodness of fit test is done with the following statistic:

χ²= ∑
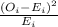`((O_i-E_i)^2)/(E_i)` ≈χ²
`_(k-1)`

Where k represents the number of categories of the study variable. In this example k= 6.

Remember, the rejection region for the Chi-square tests of "goodnedd of fit", "independence", and "homogeneity" is allways one-tailed to the right. So you will only have one critical value.

χ²
`_(k-1; 1 - \alpha )`

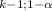
χ²
`_(6-1; 1 - 0.05 )`

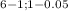
χ²
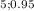`_(5; 0.95 )` = 11.070

This means thar the rejection region is χ² ≥ 11.07

If the Chi-Square statistic is equal or greather than 11.07, then you reject the null hypothesis.

2)

The statistic for the goodness of fit is:

χ²= ∑
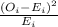`((O_i-E_i)^2)/(E_i)` ≈χ²
`_(k-1)`

Degrees of freedom: χ²
`_(k-1)`

In the example: k= 4 (the variable has 4 categories)

χ²
`_(4-1)` = χ²
`_(3)`

The statistic for the independence test is:

χ²= ∑∑
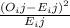`((O_ij-E_ij)^2)/(E_ij)` ≈χ²
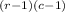`_((r-1)(c-1))` ∀ i= 1, 2, ..., r & j= 1, 2, ..., c

If the information is in a contingency table

r= represents the total of rows

c= represents the total of columns

In the example: c= 2 and r= 2

Degrees of freedom: χ²
`_((r-1)(c-1))`

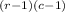
χ²
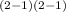`_((2-1)(2-1))` = χ²
`_(1)`

The goodness of fit test has more degrees of freedom than the independence test.

3)

To calculate the expected frecuencies for the independence test you have to use the following formula.

`e_(ij) = n * P_i. * P_.j = n * (o_i.)/(n) * (o_.j)/(n)`

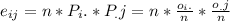
Where o_i. represents the total observations of the i-row, o_.j represents the total of observations of the j-column and n is the sample size.

Now, this is for the expected frequencies in the body of the contingency table, this means the observed and expected frequencies for each crossing of categories is not the same.

On the other hand, you would have the totals of each category and population in the margins of the table (subtotals), this is the same when looking at the observed frequencies and the expected frequencies. Wich means that the expected frequency for the total of a population is the same as the observed frequency of said population. A quick method to check if your calculations of the expected frequencies for one category/population are correct is to add them, if the sum results in the subtotal of that category/population, it means that you have calculated the expected frequencies correctly.

The expected frequency for the total of females is 80

Using the formula:

(If the females are in a row)
`e_(females.) = 100 * (80)/(100) * (0)/(100)`

`e_(females.) = 80`

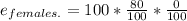
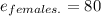
4)

There are two ways of writing down a null hypothesis for the independence test:

Way 1: using colloquial language

H₀: The variables X and Y are independent

Way 2: Symbolically

H₀:
`P_(ij)= P_(i.) * P_(.j)` ∀ i= 1, 2, ..., r and j= 1, 2, ..., c

This type of hypothesis follows from the definition of independent events, where if we have events A and B independent of each other, the probability of A and B is equal to the product of the probability of A and the probability of B, symbolically: P(A∩B) = P(A) * P(B)

5)

In this example, you have an independence test for two variables.

Variable 1, has 3 categories

Variable 2, has 4 categories

To follow the notation, let's say that variable 1 is in the rows and variable 2 is in the columns of the contingency table.

The statistic for this test is:

χ²= ∑∑
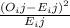`((O_ij-E_ij)^2)/(E_ij)` ≈χ²
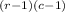`_((r-1)(c-1))` ∀ i= 1, 2, ..., r & j= 1, 2, ..., c

In the example: c= 3 and r= 4

Degrees of freedom: χ²
`_((r-1)(c-1))`

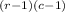
χ²
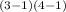`_((3-1)(4-1))` = χ²
`_(6)`

I hope you have a SUPER day!