Question

A spring oscillator is designed with a mass of 0.231 kg. It operates while immersed in a damping fluid, selected so that the oscillation amplitude will decrease to 1.00% of its initial value in 9.43 s. Find the required damping constant for the system.

Answer 1

0.05508 kg/sec

Step-by-step explanation:

mass of the oscillator m= 0.231 Kg

amplitude of oscillation given by

`A=A_0e^(-It)`

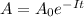
Ao= maximum amplitude

t= time and 1.00% of its initial value in t= 9.43 s.

A= 0.01Ao

⇒0.01=e^(-I×9.43)

ln100= 9.43×l

l=0.4883

we know that l= c/2m

c= damping constant

c= 2ml

=2×0.231×0.4883

=0.05508 kg/sec

Answer 2

.487 s⁻¹

Step-by-step explanation:

Let damping constant be τ . The equation of decreasing amplitude can be written as

A = A₀
`e^{-\tau t`

A / A₀ =
`e^{-\tau t`

At t = 9.43 s , A / A₀ = .01

.01 =
`[e^{-\tau*9.43`

ln.01 = - 9.43 τ

-4.6 = -9.43τ

τ = .487 s⁻¹