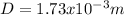Question

A large storage tank, open to the atmosphere at the top and filled with water, develops a small hole in its side at a point 16.0 m below the water level. If the rate of flow from the leak is 2.50×10−3m3/min, determine the diameter of the hole.

Answer 1

The diameter of the hole is
`1.73 x10^(-3)m`

Step-by-step explanation:

The velocity at the top of the tank is zero. As depth increases, velocity increases, thus, potential energy is equal to the kinetic energy at the hole level (16-meter depth).

Step 1: We calculate the velocity of water at the hole level

ρgh = ρv²/2

gh = v²/2 (striking the density of water out)

Therefore,

`v=√(2gh)`

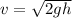
v² = (2)(9.81 m/s²)(16 m)

∴ v = 17.7 m/s (velocity of water at the hole level)

Step 2: We find the area of the hole itself.

`Area=(Volumetric flow rate)/((velocity)(time))`

`Area=(2.50x10^(-3) m^(3)/min )/((17.7 m/s)(60 s))`

`Area=2.35x10^(-6) m^(2)`

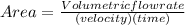
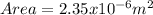
Step 3: We calculate the diameter of the hole from its area.

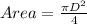
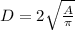
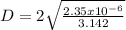
`Area=(\pi D^(2) )/(4)`

`D=2\sqrt{(A)/(\pi) }`

`D=2\sqrt{(2.35x10^(-6) )/(3.142) }`

∵
`D=1.73x10^(-3) m`

Answer 2

1.74 × 10^-3 m ( 1.74 mm)

Step-by-step explanation:

Using Torricelli"s equation to calculate the speed of water at the surface of the hole and assuming that the speed of water at the surface of the tank is zero

v ( speed of water at the surface of the hole) = √ 2g(h1 - h2) where h1 - h2 is the difference in height which 16 m

v = √ 2×9.81×16 = 17.72 m/s

work done in ( m³/s) = 2.5 × 10^ -3 / 60 seconds = 4.2 × 10^-5 m³/s

work done = A × v

4.2 × 10^-5 = A × 17.72

4.2 × 10^-5 / 17.72 = A

2.37 × 10^-6 = A where A is assumed a circle ( πr²)

r = 2.37 × 10^-6 / π = √2.37 × 10^-6 / 3.142 = 0.869 × 10 ^ -3

diameter = 2r = 2 × 0.869 × 10^-7 = 1.74 × 10^-3 m