Question

The number of stamps that Kaye and Alberto had were in the ration of 5:3 respecctively. After Kaye gave Alberto 10 of her stamps, the ration of the number of Kaye had to the number of Alberto had was 7:5. As a result of the gift, Kaye had how many more stamps than AlbertoA. 20B. 30C. 40D. 60E. 90

Answer 1

Answer: The correct option is

(D) 60.

Step-by-step explanation: Given that the number of stamps that Kaye and Alberto had were in the ration of 5:3 respectively.

After Kaye gave Alberto 10 of her stamps, the ration of the number of Kaye had to the number of Alberto had was 7:5.

We are to find the number of stamps that Kaye had more than Alberto.

Let the number of stamps Kaye and Alberto has are 5x and 3x respectively.

Then, according to the given information, we have

`(5x-10):(3x+10)=7:5\\\\\Rightarrow (5x-10)/(3x+10)=(7)/(5)\\\\\Rightarrow 25x-50=21x+70\\\\\Rightarrow4x=120\\\\\Rightarrow x=(120)/(4)\\\\\Rightarrow x=30.`

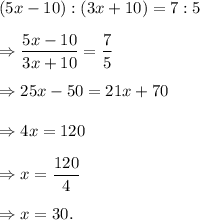
So, the number of stamps that Kaye had = 5 × 30 = 150

and

the number of stamps that Alberto had = 3 × 30 = 90.

Therefore, the number of stamps that Kaye had more than Alberto is

`150-90=60.`

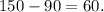
Thus, Kaye had 60 stamps more than Alberto.

Option (D) is CORRECT.