Answer:
A.
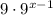
C.
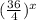
Explanation:
Given:
The given expression is
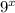
Let us simplify each choice and check whether they simplify to
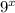 or not.
or not.
Choice A:
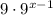
We use the law of indices:
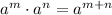
Therefore,
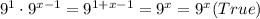
Choice B:

We use the law of indices:
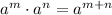
Therefore,
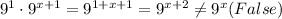
Choice C:
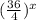
We simplify the fraction inside the parenthesis. So,
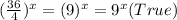
Choice D:
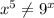
Choice E:
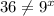
Therefore, the correct options are A and C.