Answer: Area of the white region is 51.9 square cm
Explanation:
The given circle has a radius of 7cm.
Step 1: Calculate the area of complete circle
The area of circle is given as A=
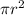
A=
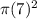
A=
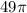
Step 2: Calculate the area of a small segment of circle making 150 degrees.
The complete circle is of 360 degree
So, Area of a small segment of circle making 150 degrees will be,
A'=(150/360)
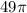
A'=64.14085
Step 3: Calculate the area of the white region
The small segment of the circle is made of a triangle in the blue and white region part
Therefore,
A'= 64.14085 = Area of triangle + Area of white region
Area of white region= 64.14085 - Area of a triangle
For the area of a triangle, two sides are equal and the radius of the circle
Therefore, It is an isosceles triangle
Area of triangle is given by = (1/2)(base)(height)
height = 7 cos (75)=1.8117
base = 2x7sin(75)=13.522
Note: Figure shown calculation of trigonometry.
Area of triangle is given by = (1/2)(1.8117)(13.522)=12.249
Area of white region= 64.14085 - Area of a triangle
Area of white region= 64.14085 - 12.249 =51.89185 square cm
Thus, the Area of the white region is 51.9 square cm