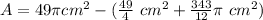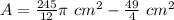Question

Mathematicians come thru wit da help

Answer 1

`A=7\pi\ cm^2-(343)/(6)\ cm^2`

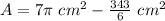
Explanation:

Area of plane figures

Being r the radius of a circle, the area of a sector defined by an angle
`\theta` is

`A_s=(\theta)/(2) r^2`

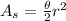
If a is the repeated side of an isosceles triangle and
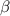`\beta` is the angle they define, then the area of the triangle is

`A_t=(a^2)/(2)sin\beta`

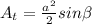
The figure shows a circle with radius of r=7 cm. The white area is equal to the area of the circle minus the blue area

The area of the circle is

`A_c=\pi r^2=49\pi cm^2`

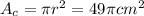
The blue area is the sum of the sector defined by the angle (360-150)=
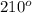`210^o` and the triangle. An angle of
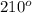`210^o` is equivalent to

`(\pi)/(180^o)210^o=(7)/(6)\pi`

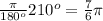
The area of the sector is

`A_s=(7)/(12)\pi (7^2)=(343\pi)/(12)\ cm^2`

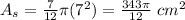
The area of the triangle with center angle 150^o is

`A_t=((7)(7))/(2)sin150^o`

`A_t=(49)/(2)(1)/(2)`

`A_t=(49)/(4)\ cm^2`

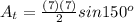
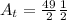
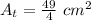
The blue area is

`(49)/(4)\ cm^2+(343)/(12)\pi\ cm^2`

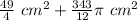
Finally, the white area is

`A=49\pi cm^2-((49)/(4)\ cm^2+(343)/(12)\pi\ cm^2)`

`A=(245)/(12)\pi\ cm^2-(49)/(4)\ cm^2`