Question

A collection of dimes is arranged in a triangular array with 17 coins in the base row, 16 in the next, 15 in the next, and so forth. Find the value of the collection.

Answer 1

153 coins will be there.

Explanation:

The number of coin in the bottom row / or last row = 17

The number of coins in the second last row = 16

|

|

|

|

The number of coins in the second row = 2

The number of coins in the first row = 1

So the total number of coins = (Number of coin in the first row) + (Number of coins in the second row) + (Number of coins in the third row) + ....... + (Number of coins in the last row / seventeenth row)

Total number of coins = 1+2+3+....+16+17

Total number of coins =
`(17*(17+1))/(2)=(17*18)/(2)=17*9=153`

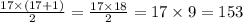
(NOTE: Sum of first n natural number =
`(\boldmath n*(n+1))/(2)`)