Question

How long does it take the Sun to melt a block of ice at 0∘C with a flat horizontal area 1.0 m2 and thickness 2.0 cm ? Assume that the Sun's rays make an angle of 32 ∘ with the vertical and that the emissivity of ice is 0.050.

Express your answer to two significant figures and include the appropriate units.

Answer 1

It takes 40 hours to melt the block of ice.

Step-by-step explanation:

According to the principles of radiation and heat transfer respectively:

ΔQ = I(dt)eAcosθ (I = Solar energy density; dt = time taken; e = emissivity; A = Area of block; θ = angle between the sun ray and the horizontal)

ΔQ = mLf (ΔQ = Heat change; m = mass of ice; Lf = Specific latent heat of fusion of ice)

but m = ρV = ρ.A.dx, therefore, the heat transfer equation can be re-written as:

ΔQ = ρ.A.dx.Lf

Lets equate the radiation equation and the modified heat transfer equation, we have:

ρ.A.dx.Lf = I(dt)eAcosθ

ρ.dx.Lf = I(dt)ecosθ (Striking out the area)

Let's make dt the subject of formula,

dt = ρ.dx.Lf /I.e.cosθ

ρ = Density of ice,
`9.2x10^(2) Kg/m^(3)`

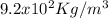
Lf =
`3.36x10^(5) J/Kg`

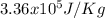
e = 0.050

θ = 32 deg. C

Now, let's substitute the terms:

`dt=((9.2x10^(2))(0.02)(3.36x10^(5) ) )/((1000)(0.050)(cos32))`

`dt=14.45x10^(4) s = (14.45x10^(4))/(3600) hr=40.14 hr`

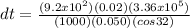
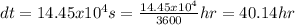
Therefore, the time taken for the ice to completely melt is 40 hours (Two significant figures)