Question

An electron in the n=7 level of the hydrogen atom relaxes to a lower energy level, emitting light of 1005 nm. Part A What is the value of n for the level to which the electron relaxed?

Answer 1

rom level n = 7 to level n = 3

Step-by-step explanation:

Bohr's model describes the energy levels for the hydrogen atom

En = -13.606 / n²

Where n is an integer with values ​​of 1, 2, 3

An electronic transition occurs between two permitted levels of energy

ΔE =
`E_(nf)` -
`E_(no)`

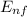Let's apply these relationships our problem.

Let's start by knowing the energy of level n = 7

E₇ = - 13.606 / 7²

E₇ = - 0.27767 eV

Now let's see what the energy of the emitted photon

E = h f

c = λ f

f = c / λ

E = h c / λ

E = 6.63 10⁻³⁴ 3 10⁸/1005 10⁻⁹

E = 19,791 10⁻²⁰ J

Let's reduce to eV

E = 19,791 10⁻²⁰ (1 eV / 1.6 10⁻¹⁹)

E = 1,237 eV

The possible transitions from this level are towards n = 6, 5, 4,3,2, 1

We must test the different values ​​until we find the right one

Energy of the states

n
`E_(n)`

6 -0.378

5 -0.544

4 -0.850

3 -1,512

2 -3,402

1 -13,606

Let's examine the transition n = 7 to n = 6

ΔE = - 0.27767 - (-0.3779)

ΔE = 0.10023 eV

n = 7 to n = 5

ΔE = -0.27767 - (-0.5442)

ΔE = 0.267 eV

n = 7 a n = 4

ΔE = -0.27767- (-0.8504)

ΔE = 0.573 eV

n = 7 a n = 3

ΔE = -0.27767 - (- 1.5118)

ΔE = 1.234 Ev

This is the transition sought, so that the electron goes from level n = 7 to level n = 3