Question

A 42-g block of copper at -13 ∘C is added to 150 g of water in a 78-g aluminum cup. The cup and the water have an initial temperature of 4.9 ∘C. Find the equilibrium temperature of the cup and its contents. What mass of ice, if any, is present when the system reaches equilibrium?

Answer 1

`T_(e) = 4.49\°C`

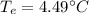
There will be no ice as equilibrium temperature does not go below 0°C (the freezing point of water.

Step-by-step explanation:

The zeroth law of thermodynamics states that if two systems are both in thermal equilibrium with a third system, they are in thermal equilibrium with each other. Thus, when the system reaches equilibrium the copper, water and aluminum cup will all be the same temperature. The sum of energy lost from the cup and water will be gained by the copper

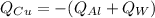`Q_(Cu)=-(Q_(Al)+Q_(W))` (eq 1)

Where:
`Q_(Cu)` is the energy gained by the copper block and
`Q_(Al)` and
`Q_(W)` is the energy lost by the aluminum cup and water respectively.

Energy change of material can be determined by its mass, specific heat capacity and temperature change

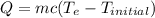`Q=mc(T_(e)-T_(initial))` (eq 2)

Where:
`m` is the mass of the substance,
`c` is the specific heat capacity,
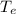`T_(e)` is the final equilibrium temperature and
`T_(initial)` is the initial temperature.

Extracting information from the question and taking specific heat capacities from thermodynamic reference tables:

Copper:

`m_(Cu)=42 g, c_(Cu)=0.385 J/g.\°C,T_(Cu, initial)= -13\°C`

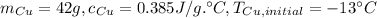
Aluminum cup:

`m_(Al)=78 g, c_(Al)=0.9 J/g.\°C,T_(Al, initial)= 4.9\°C`

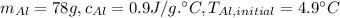
Water:

`m_(W)=150 g, c_(W)=4.186 J/g.\°C,T_(W, initial)= 4.9\°C`

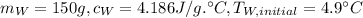
Generating expressions for energy change (unknown) at equilibrium temperature (unknown) using eq 1

`Q_(Cu)=m_(Cu)c_(Cu)(T_(e)-T_(Cu,initial))`

`Q_(Cu)=42*0.385*(T_(e)-(-13))`

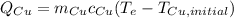
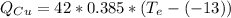
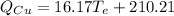`Q_(Cu)=16.17T_(e)+210.21` (eq 3)

`Q_(Al)=m_(Al)c_(Al)(T_(e)-T_(Al,initial))`

`Q_(Al)=78*0.9*(T_(e)-4.9})`

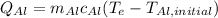
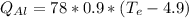
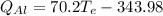`Q_(Al)=70.2T_(e)-343.98` (eq 4)

`Q_(W)=m_(W)c_(W)(T_(e)-T_(W,initial))`

`Q_(W)=150*4.186*(T_(e)-4.9)`

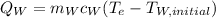
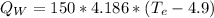
`Q_(W)=627.9T_(e)-3076.71` (eq 5)

Substituting eq 3, 4 and 5 in eq 1 and solving for
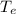`T_(e)` gives the temperature at equilibrium:

`Q_(Cu)=-(Q_(Al)+Q_(W))`

`16.17T_(e)+210.21 = -(70.2T_(e)-343.98+627.9T_(e)-3076.71)`

`16.17T_(e)+210.21 = 3420.69-698.1T_(e)`

`16.17T_(e)+698.1T_(e) = 3420.69-210.21`

`714.27T_(e) = 3210.48`

`714.27T_(e) = 3210.48`

`T_(e) = 4.49\°C`

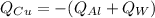
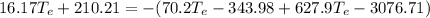
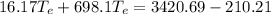
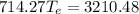
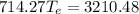
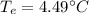
The freezing point of water is 0°C. As the equilibrium temperature is above the freezing point of water, no ice will be present